Fresh Meat II: The Challenge Episode #4

My earlier posts on the MTV reality show Fresh Meat II: The Challenge recommended two strategies for the competing factions in the show: one side should tighten the bounds in its group and keep loyalty strong while the other side should use the threat throwing a team into the elimination challenge as a way to get teams to defect to their faction. However the factions got the strategies backwards. I recommended Kenny's alliance use the threat of being sent into the elimination challenge to get someone to defect to his alliance. Wes's coalition had the superior numbers. It was in Wes's coalition's best interests to keep loyalty strong within the group. Instead Kenny let someone in his alliance choose who was going into the elimination challenge, thus trying to boost loyalty withing the group while Wes's coalition used the threat of being thrown into the elimination round to get a team to defect to his coalition.



I'm not sure why Kenny--once again--did not use the threat of sending someone into the elimination round as a tool to get a team to defect to his alliance. He seems smart enough. Maybe his arrogance and strong results in the reward challenges--more on this later--are deterring him.

I thought the strategy used by Wes's coalition--using the threat of the elimination challenge to get a team to defect--was somewhat valid but not for the reason's Eve suggested. Eve thought it was a good idea as it would peel a team away from Kenny's alliance. As I wrote in an earlier post, Kenny's alliance already had too few teams to be much of a threat. Wes' coalition didn't need to get bigger; it just needed to stay together. Eve's action undermined the coalition and pissed off two teams (CJ and Landon's teams) which had the show ending with those teams considering defecting to Kenny's alliance. However the move was valid in that it kept Kenny from choosing Eve's team to go into the elimination challenge. Removing that risk and uncertainty was a worthwhile goal for Eve to pursue. As long as she felt that the risk of her losing the elimination challenge was greater than the risk of her coalition falling apart, it was a good move. If that was not the case though then she was just plain scared.

Back to Kenny and Laurel's prowess at the reward challenges. They certainly look like a strong team. Laurel has performed much better than the rest of the females in the challenges (and she may be the best looking one too). In my earlier posts, my calculations assumed that each team had an equal shot of winning the reward challenge. Now that Kenny's  team has won 3 out of the 4 reward challenges is that assumption still valid?

Let's use the binomial distribution to test the assumption. The binomial distribution forces the probability for each trial to be set at a fixed probability p. Even though the number of teams changes after each elimination challenge as a team is sent home and thus p changes for each reward challenge (ie if you are 1 of 2 teams you have a 50% chance of winning but if you are 1 of 10 teams you only have a 10% chance of winning). I am going to fix the probability p at 9%. The number of teams in the reward challenges has been 12 (p = 8.3%), 11 ( p = 9.1%), and 10 (p = 10%) so 9% is about right. Here's the binomial theorem:

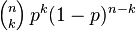
p = .09; n is the number of reward challenges so far which is 4; k is the number of times Kenny's team has won the reward challenge. I am going to calculate the theorem for k = 3 and k = 4 since if Kenny's team had won all 4 challenges I would also be doing this little test. Popping this into an spreadsheet, the probability of Kenny's team winning 3 or 4 challenges out of 4 challenges--assuming they only had a .09 chance of winning a reward challenge--is a tiny 0.3%.

The math is a little more complicated than the above calculation. If we had chosen one particular team apriori of the show's first episode and done the above calculation than the 0.3% number would have been correct. However there were 12 teams to start the show so any one of them could have been the team to win 3 out of the first 4 challenges. What are the odds that none of them would have won 3 out of the first 4 challenges? I believe we can use the Bonferroni Inequality to get an approximation:
1 - (1 - 0.3)^12 = 3.2%
Assuming that all the teams had an equal chance of winning the reward challenge, 3.2% of the time 1 of the 12 teams would win 3 or 4 out of the first 4 challenges. 0.3% and 3.2%. Either way it is safe to conclude that Kenny's team has a better than equal chance of winning the reward challenges and thus may assumption in earlier posts was incorrect.

Even with Kenny's team having a better chance than I had assumed at winning the reward challenges, his alliance was still in a very unfavorable position. His alliance had to win 3 elimination challenges in a row just to even the amount of teams in each faction. I calculated the probability of that happening at a low 12.5%. Still unfavorable, just not as dire as I had thought.

On an aside is there a distribution that allows the p to change after each trial and would work better than the binomial in this case?